Dual path biphasic column for highly selective and ultrafast organic solvent membrane extraction

Materials

The α, ω-RCOOH PDMS (M_w = 1k g mol⁻¹, DMS-B12) was purchased from Gelest (Morrisville, PA, USA), while the ω-RCOOH PDMS (M_n = 1 k g mol⁻¹, P18578-DMS-C10COOH), ω-RCOOH PBd (M_n = 1.9 k g mol⁻¹, P19257-BdCOOH), and ω-RCOOH PS (M_n = 1.4 k g mol⁻¹, P18083-SCOOH) were purchased from Polymer Source (Dorval, QC, Canada). Aluminum chloride hexahydrate (ReagentPlus, 99%), cyclohexane (anhydrous, 99.5%), sodium hydroxide solution (50 % in H₂O), Span 80, silicone oil (viscosity 5 cSt), acrylamide (≥99%), N, N’-methylenebisacrylamide (99%), Irgacure 2959 (98%), and Nile Red were all generally provided from MilliporeSigma (St. Louis, MO, USA). The seven drug molecules, scoparone (98%), 11-deoxycorticosterone (≥97%, HPLC), spironolactone (97–103%), homoharringtonine (≥98%, HPLC), cucurbitacin E (≥95%, HPLC), hypaconitine ( ≥98%, HPLC), and tilmicosin (analytical standard), were also provided from MilliporeSigma. Aluminum triacetate was obtained from Shanghai Aladdin Biochemical Technology (Shanghai, China).

Al-COO interfacial complex formation

For the oil phase, the RCOOH-terminated polymers were dissolved in cyclohexane at concentrations ranging from 10⁻¹ to 10¹mM. For the aqueous phase, aluminum chloride hexahydrate was dissolved in deionized (DI) water (18.2 MΩ·cm) at a concentration ranging from 10⁻² to 5 mM, and the solution was then titrated to pH 5.8 by gradually adding 1 M sodium hydroxide aqueous solution. The pH was monitored using a pH meter (Orion Star A215, Thermo Fisher Scientific, MA, USA). The titrated solution was allowed to equilibrate for 12 hours before use. Since the pKa of RCOOH is ≈4.8³⁴, maintaining a pH of 5.8 or higher ensures that most (≥≈90 %) of the RCOOH in contact with the aqueous phase is deprotonated (Supplementary Fig. 10a). In contrast, the fraction of Al³⁺ out of the Al species in the aqueous phase decreases with increasing pH owing to hydrolysis equilibrium (Supplementary Fig. 10b)³⁵, making pH 5.8 considered optimal for complexation. The maximum concentration of Al allowing titration to pH 5.8 is 5 mM (Supplementary Fig. 10c). When an interface is created between the oil and aqueous phases, Al³⁺ and the RCOO⁻ begin to complex at the interface, and the Al-COO complex is believed to be fully developed after 2 mins (Supplementary Note 1). To produce the water-in-oil emulsion stabilized with the Al-COO complexes, a 1:1 mixture of the aqueous phase (5 mM) and oil phase (10 mM), 2 mL of each phase in an 8 mL glass vial, was emulsified using a vortex machine (VM-30, Daihan Scientific, Republic of Korea) at 3000 rpm for 5 mins.

Pendant drop analysis

After positioning the tip of a needle (7770-02, Hamilton, NV, USA), mounted on a glass syringe (50 μL, 7637-01, Hamilton) containing the oil phase (10 mM), near the middle of a disposable acrylic cuvette (1 × 1 × 5 cm³, 01960-00, Daihan Scientific) filled with 3 mL of the aqueous phase (5 mM), the oil phase was carefully injected to form an oil drop (≈10–30 μL) hanging from the tip. Images of the drop were captured over time at a rate of two images per min using a CCD camera (WAT-902H, Watec) and then analyzed using custom MATLAB code to extract information about the interfacial tension. More details about the pendant drop method are explained by Berry et al.³⁶ To compress or expand the interface, the pendant drops were gently withdrawn or infused, respectively.

Interfacial rheology

Interfacial rheometry utilizing a biconical measuring probe³⁷ was employed. A biconical measuring probe (BI-C68-5, Anton Paar, Austria) and a sample holder (14339, Anton Paar) were mounted on a conventional rheometer (MCR 302, Anton Paar). The Al-COO complex was formed by gently placing the oil phase (10 mM, 6.6 mL) using a pipette on the air-aqueous phase (5 mM, ≈100 mL) interface where the measuring probe was located, ensuring that the base of the measuring probe was in contact with the interface between the oil and aqueous phases. After a 2 min aging time, an amplitude sweep was performed in the range of strain (γ) from 10⁻¹ to 2 · 10¹% at a fixed frequency (f) of 10⁰Hz, and a frequency sweep was performed in the f range from 10⁻¹ to 10¹Hz at a fixed γ of 10⁻¹%. A time sweep was performed under the conditions (γ = 0.1% and f = 1 Hz) that fell into the linear regime in the amplitude sweep (Supplementary Fig. 11a), as soon as the oil phase was placed. For reliable interfacial rheometry, the dimensionless Boussinesq number (Bo) of the system should be large enough, typically at least 10. Bo is defined as the drag force from an interface over that from bulk, and is estimated by

where η*_s and η*_b are the complex viscosities of the interface and bulk, respectively, and P_c and A_c are the contact perimeter and area, respectively³⁸. The measuring probe consists of two symmetric cones with a base diameter of 6.8 cm and an opening angle of 85 °, which yields A_c/P_c ≈ 1.7 cm. Additionally, both viscosities (η_bs) of the oil and aqueous phases were measured to be 1 mPa·s using a double-gap probe (DG 26.7, Anton Paar) mounted on the rheometer. Given that the η_bs do not depend on the shear rate, both phases are Newtonian fluids, and thus the η_bs can be used as the η*_b³⁸. Given the values of η*_b and A_c/P_c, the η*_s should be greater than 3.4 · 10⁻¹ mPa·m · s for reliable interfacial rheometry. The complex modulus (G*_s = G’_s + iG“_s) is related to η*_s as G*_s = 2πf η*_s³⁸, and all our measurements were more than 10 times greater than this limit G*_s.

Deposition of the Al-COO complexes and atomic force microscopy

The Al-COO complex formed at the interface was deposited on a substrate using the popular inverse Langmuir-Schaefer method³⁹. To prepare the substrate, a silicon wafer (WSI0PR0029, iTASCO, Republic of Korea) cleaved into ≈2 × 2 cm² was rinsed with isopropyl alcohol (99.5 %, Samchun, Republic of Korea) and DI water. The rinsed wafer was then placed in a cylindrical glass cuvette (diameter = 50 mm, height = 30 mm) at an angle of ≈45 °. Next, 20 mL of the aqueous phase (5 mM) was introduced using a pipette, followed by gentle placing of 3 mL of the oil phase (10 mM) on top, triggering complexation. After aging for the desired time, the aqueous and oil phases were sequentially sucked out from the bottom at a rate of ≈10 mL/min by an aspirator, leading to the deposition of the Al-COO complex onto the submerged substrate as the interface descended and contacted the substrate. It is noteworthy that a small amount of the aqueous phase may be trapped between the substrate and Al-COO complex when the substrate is placed in the cuvette without tilting. Finally, nitrogen was blown over the deposited film to remove any remaining oil phase. The thickness of the Al-COO complex film was measured using an atomic force microscope (XE-100, Park Systems, Suwon, Republic of Korea) equipped with an etched silicon cantilever (NCHR, Nano World, Neuchâtel, Swiss) at a resonance frequency of 250–390 kHz and force constant of 21–78 N/m. The scan area and rate were 0.5 × 0.5 μm² and 0.6–0.8 Hz, respectively.

GIWAXD

To examine the nanostructure of the Al-COO complex, the film prepared using the method described in the preceding section with a constant aging time of 30 minutes underwent GIWAXD analysis. The experiments were carried out at beamline 9A-USAXS at the Pohang Accelerator Laboratory (PAL, Republic of Korea). The two-dimensional diffraction experiment was performed at a grazing incidence angle of 0.08 degrees (≈1.4 mrad) using a CuK_α beam source (11.09 keV), with diffraction patterns collected by a MAR CCD detector at room temperature. The sample-to-detector distance was set to 220 mm. Prior to analysis, background calibration was conducted using a sucrose standard sample.

IR spectroscopy and XPS

For IR spectroscopy, multiple Al-COO complexes were deposited onto the cleaved silicon wafer by casting the emulsion stabilized with the Al-COO complexes. The emulsion was prepared following the procedure outlined in the interfacial complex formation section (METHODS), and 30 μL of the emulsion was subsequently placed onto the rinsed, cleaved silicon wafer. As the solvents evaporated, the Al-COO interfacial complexes stacked on the wafer. As a reference IR spectrum, the α, ω-RCOOH PDMS, a viscous liquid, was cast between two zinc selenide disks (160-1304, PIKE Technologies, Madison, WI, USA). A Fourier-transform infrared spectrometer (NicoletTM iSTM 50, Thermo Fisher Scientific) operating in transmission mode was used to measure the infrared absorbance of each sample at the wavenumber range 650–4000 cm⁻¹. For XPS analysis, the Al-COO complex film was prepared following the same manner used for atomic force microscopy. Aluminum triacetate, serving as a reference material, was thinly and evenly applied onto a double-sided adhesive copper tape attached to the cleaved silicon wafer. The binding energies of the 2p orbital of Al in the Al-COO complex and aluminum triacetate were analyzed using an X-ray photoelectron spectrometer (K-Alpha, Thermo Fisher Scientific) equipped with an Al source (1486.6 eV) at 4 × 10⁻⁶Pa. The binding energy of each spectrum was corrected accordingly by shifting the C 1 s peak of maximum intensity to 284.8 eV.

Real-time measurement of molecular extraction from the oil phase to the aqueous phase

The extraction of the drug molecules from the oil phase to the aqueous phase was monitored in real-time by measuring the UV absorbance of the extracted molecules in the aqueous phase at a specific wavelength (λ_peak, Table 1) using a UV-vis spectrometer (UV-2600, Shimadzu, Japan). To correlate the UV absorbance and the concentration of the drug molecules, measurements were carried out under conditions where a linear relationship between them was established, adhering to the Beer-Lamber law (Supplementary Fig. 12). For the extraction across the bare interface, 1.0 mL of the aqueous phase was transferred into a quartz UV cuvette (12.5 × 12.5 × 45.0 mm³, DH.Cel1511, Daihan Scientific), followed by the careful addition of 1.0 mL of the cyclohexane solution containing the drug molecules within the concentration range of 10²–10³μM to the top of the aqueous phase. The cuvette was sealed with a Teflon cap to prevent solvent evaporation and then taken to the spectrometer for monitoring. Throughout the monitoring, the distribution of the extracted molecules in the aqueous phase was maintained uniformly through continuous mixing using a magnetic stirrer (Spinette Cell Stirrer, Starna Cells, Inc., CA, USA) and a stirring bar (5 mm × 2 mm, Starna Cells, Inc.) placed beforehand in the aqueous phase. For the extraction across the Al-COO complex, only the way of adding the oil phase slightly differed. Initially, 0.5 mL of the oil phase was added and allowed to sit for at least 3 mins to form the Al-COO complex. Subsequently, another 0.5 mL of the oil phase containing the drug molecules was gently added, and the mixed oil phase was carefully agitated using a pipette tip by hand. The UV absorbance data measured over extraction time were converted to the drug concentration in the permeate (C) and normalized by the equilibrium drug concentration in the permeate without the interfacial complex (C_eq), and rejection is represented by the steady-state value of (1−C/C_eq) × 100%.

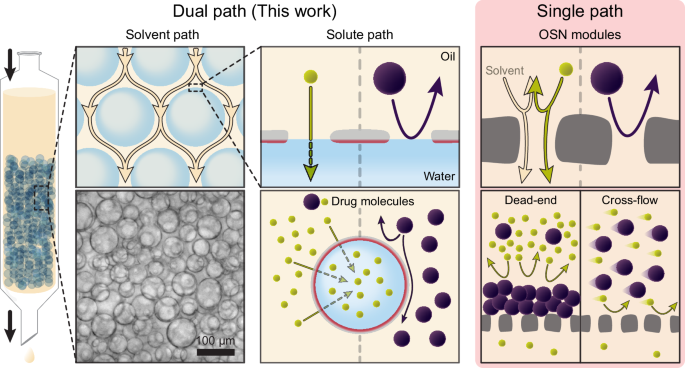
Separation of molecules in organic solvents using the column

After adding acrylamide, N, N’-methylenebisacrylamide, and Irgacure 2959 to the aqueous phase at concentrations of 5.0, 0.2, and 0.3 wt %, respectively, as the monomer, crosslinker, and photo initiator, a water-in-oil emulsion was generated following the procedure outlined in the interfacial complex formation section (METHODS). This emulsion was then subjected to curing for 30 mins in a UV curing chamber (RX-H1500dst, Raynics, Republic of Korea) before being transferred to a glass column (SL.Col2040.1, Daihan Scientific) with inner dimensions of 10 mm in diameter and 200 mm in height. The glass column featured a PTFE stopcock at the outlet and an internal glass filter, which supported the hydrogel extractors but passed the continuous (oil) phase, and was connected to a vacuum pump (PU-300, Daihan Scientific) and a flask, as shown in Fig. 3a. A negative pneumatic pressure of 0.3 bar applied by the pump facilitated the exit of the continuous phase, causing the extractors to pack closely together on top of the filter. After that, the 5 mL of cyclohexane solutions containing the drug molecules were injected at the top of the column and then pressurized by the pump to pass through the extractor packing and exit the column. The average z-directional solvent velocity (v_z) is calculated by dividing the initial height of the 5 mL cyclohexane solution in the column by the time spent on the extraction. The disparity in molecule concentration before and after passage through the column was assessed via UV absorbance analysis.

Microscopy

To visualize the emulsion via fluorescence microscopy, the oil phase, additionally containing Nile Red, a fluorescent dye, was used. The generated emulsion was carefully poured into a cylindrical glass cuvette (diameter = 50 mm, height = 30 mm) in a small amount (ca. 0.2 mL) and then thinly spread. The cuvette was sealed with a glass cap to prevent evaporation of the oil phase and subsequently positioned on an inverted microscope (IX73, Olympus, Japan) equipped with an iXon EMCCD camera (X-6880, Andor Technology, UK). The microscope was operated in transmission mode, and the images captured by the camera were analyzed using software (Andor solis) provided by Andor Technology. The presence of Nile red in the oil phase was detected through the AT560/635 filter (39010, Chroma Technology Corp., Bellows Falls, VT, USA), enabling the distinction of each phase. The images of the column packed with the extractors were acquired using the same microscope but in optical reflection mode. The microstructure of the extractors was analyzed using a field emission scanning electron microscope (FE-SEM, S-4800, Hitachi, Japan) at 5 kV electron beam voltage. To ensure high-resolution imaging, the samples were coated with a 10 nm layer of platinum using a sputter coater (SPT-20, COXEM Co., Ltd., South Korea), enhancing electron conductivity.

Details in the CFD simulation

To investigate the kinetics of column-scale OSME reactions, we conducted a reactive fluid dynamics simulation using COMSOL Multiphysics software. The simulation modeled solvent flow behavior and reaction kinetics around the extractors in the column. A single-phase simulation incorporating drug concentration was used to describe the flow behavior, while the extractor surface was treated as a fixed solid boundary, with extraction from the solvent assumed to occur as a surface reaction.

The simulation geometry consisted of two distinct domains, as illustrated in Supplementary Fig. 13a. The upper domain, highlighted in blue, represented the solvent region with a high initial drug concentration, where no reaction occurred. The lower domain depicted the packed extractors within the column, where extraction took place. The geometry was designed with a height of 5 mm for each domain and a column radius of 0.24 mm. The extractors, with a diameter of 42.8 µm, were arranged in a hexagonal packing configuration, maintaining an inter-particle distance to achieve a volumetric fraction of 69%.

The governing equations for the incompressible Newtonian fluid flow include the momentum conservation equation:

and the mass conservation equation:

where u is the flow velocity, p is the pressure, ρ is the fluid density, and μ is the fluid viscosity. Given that the flow rate was within the Laminar flow regime (Reynolds number Re = ρuL · μ⁻¹ L is the characteristic length), turbulent effects were not included in the simulation. The fluid properties used in the simulation were set to match those of cyclohexane (μ = 1 cP, ρ = 779 kg/m³). Since the viscosity of the solution was assumed to be independent of chemical concentration, the flow was considered steady. Following the determination of the flow field, chemical reaction and convection were calculated. The simulation mesh was constructed using the fine option of the mesh builder, highlighted in red markers in Supplementary Fig. 14. The inlet flow rate was set to match the average z-directional flow rate observed at experiments (v₀ = 2 × 10⁻¹mm/s). For boundary conditions, a no-slip condition was applied to all surfaces except for the cross-sections where symmetric boundary conditions were used, as indicated by the red solid line in Supplementary Fig. 13c.

The mass conservation equation for the chemical concentration of the drug molecule (c) is described by

where J = − D∇c is the diffusion flux within the continuous fluid’s flow, D is the diffusion coefficient, and R_s represents the reaction term. At the boundaries between the extractor and the continuous fluid,

where J_s is the surface penetration flux and n is the normal vector at the boundary. The surface penetration flux is connected to the drug molecule’s surface concentration. The mass conservation of the surface concentration (c_s) on the extractor is defined as a function of the degree of reaction (θ) by the following equations,

where k is the first order reaction constant, and Γ_s = Kc₀d_p/6 is the maximum surface concentration. Here, K is the partition coefficient, c₀ = 700 μM is the initial concentration of the drug molecule at the upper phase, and d_p is the diameter of the extractor. The maximum surface concentration was calculated from the volumetric concentration at the maximum penetration, and different k values correspond to different K as shown in Supplementary Table 1. For the inlet boundary, it was assumed at the top surface of the upper phase with pure solvent (c = 0).

As shown in Supplementary Fig. 15, the amount of drug molecules decreased linearly over time, regardless of variations in flow rate and partition coefficient. The linear reduction also held true when the column and drug molecule volumes were scaled up, demonstrating that the same flow rate and penetration reaction were maintained across different scales, including in the radial direction. To compare the computational simulation with experimental results qualitatively, the S in Fig. 4 was calculated as the ratio of the remaining drug molecule amount left (C₀–C_drop) to the initial drug molecule amount (C₀) for a 5 mL solution, where

Here, C_drop is the amount of drug molecules extracted into the extractors, τ_ret is the retention time, and Φ_s(t) is the volumetric drug consumption rate, given by:

where J_s(t) is the surface penetration flux at time t and dV is the differential volume element. The ratio of the experimental to computational column diameter, ξ was calculated as

The pre-factor 1.1 was introduced to account for the volume fraction difference between the simulation and the experiment.